Outstanding Tips About How Many Resistors Should Be Connected In Parallel

A Resistor Has Resistance Of 176 Ohms. How Many These Resistors
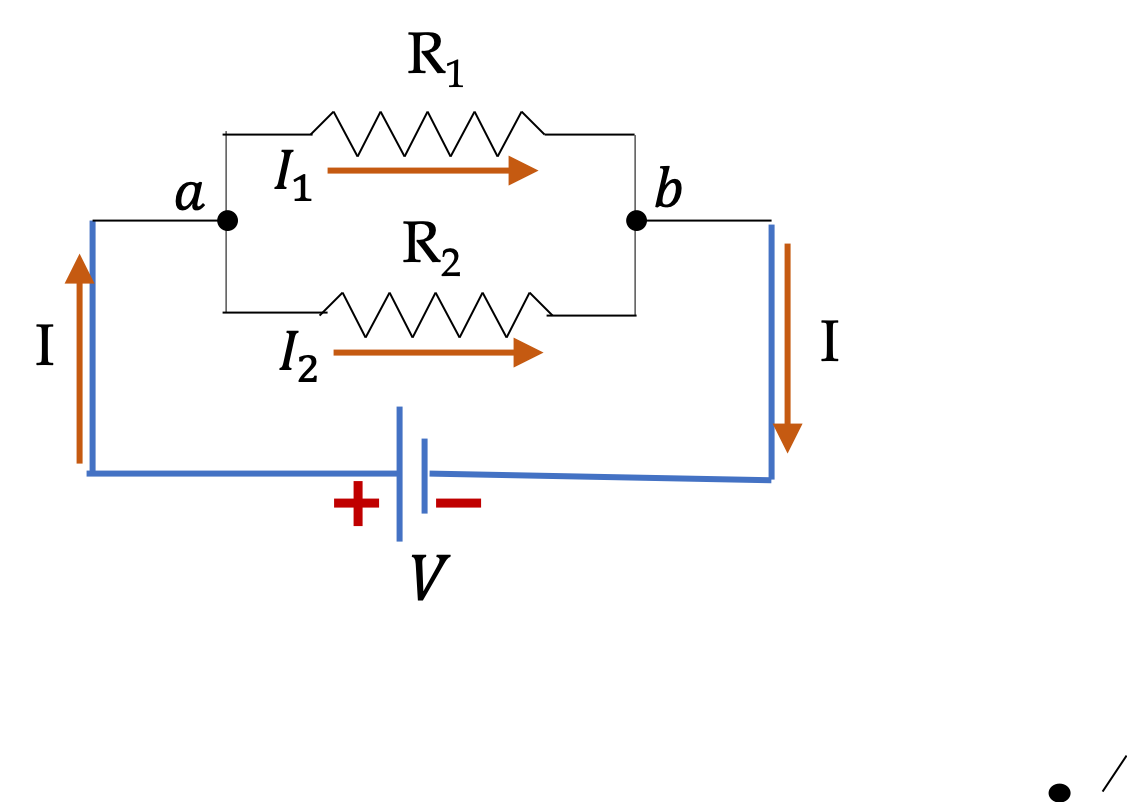
Parallel Resistors
1. Understanding the Basics
So, you're staring at a bunch of resistors and the ominous question “How many should I connect in parallel?” Well, fear not! We're not diving into the abyss of complex circuit theory right away. Instead, let's break down the core concept: connecting resistors in parallel is like adding lanes to a highway for electrons. The more lanes (resistors), the easier it is for the current (electrons) to flow. This effectively reduces the overall resistance of the circuit.
Imagine trying to get a crowd of people through a narrow doorway versus a wide, open gate. The doorway is like a high-resistance resistor, making it hard for current to pass. The gate is like several resistors in parallel, providing multiple paths and lowering the overall resistance. This is how current flows and is the basic concept of parallel resistors.
Why would you even want to reduce resistance? Plenty of reasons! Maybe your circuit needs to draw more current than a single resistor allows, or perhaps you need a very specific resistance value that isn't available in a single component. Whatever the reason, understanding parallel resistors is crucial for any electronics enthusiast.
Think of it this way: a single resistor is like a grumpy tollbooth operator slowing down traffic. Adding more in parallel is like opening up more tollbooths; the traffic flows much faster, and the overall resistance to the flow is lower. So, how many tollbooths (resistors) should you open? Let's delve deeper!

The Magic Formula (It's Not Actually Magic)
2. Calculating Equivalent Resistance
Alright, let's get down to the nitty-gritty just kidding! We'll keep it simple. The formula for calculating the total (or equivalent) resistance of resistors in parallel is this:
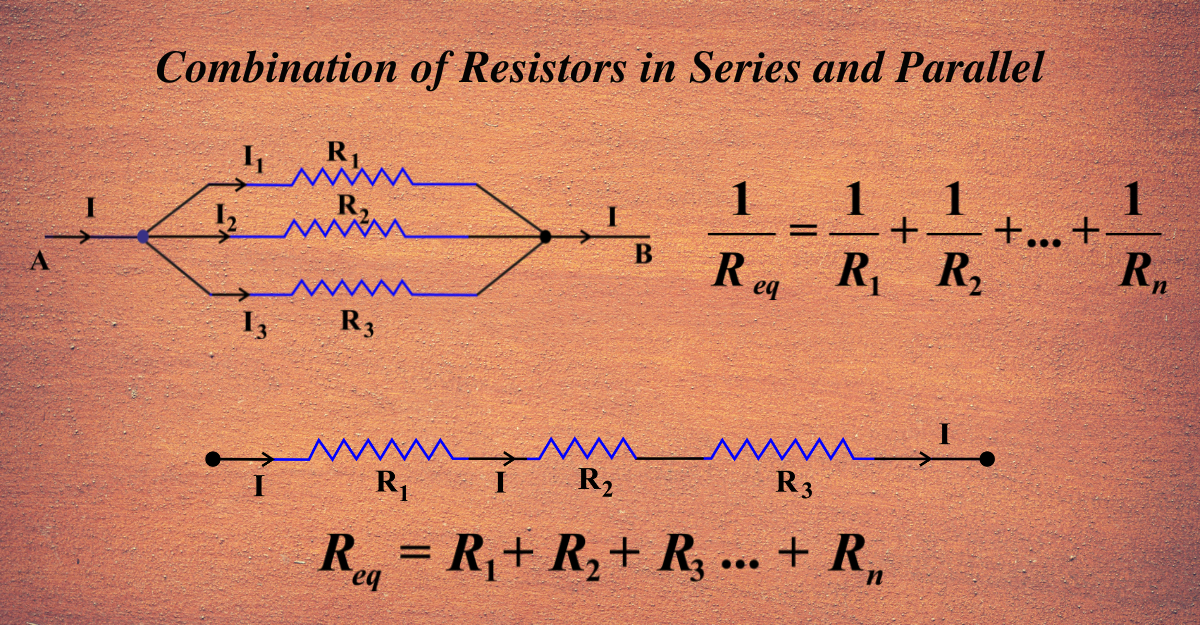
1/Rtotal = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn
Where Rtotal is the total resistance, and R1, R2, R3, and so on are the resistances of the individual resistors connected in parallel. This might look scary, but trust me, it's easier than assembling IKEA furniture. To find Rtotal, you need to calculate the sum of the reciprocals of each resistance, and then take the reciprocal of that sum.
For example, let's say you have two 100-ohm resistors in parallel. The calculation would be: 1/Rtotal = 1/100 + 1/100 = 2/100. Taking the reciprocal, Rtotal = 100/2 = 50 ohms. Notice how the total resistance (50 ohms) is lower than either of the individual resistors (100 ohms). This is the key takeaway!
If all your resistors are the same value (like the two 100-ohm resistors above), the formula simplifies even further: Rtotal = R / n, where R is the value of each resistor and n is the number of resistors. So, for three 100-ohm resistors in parallel: Rtotal = 100 / 3 = 33.33 ohms (approximately).
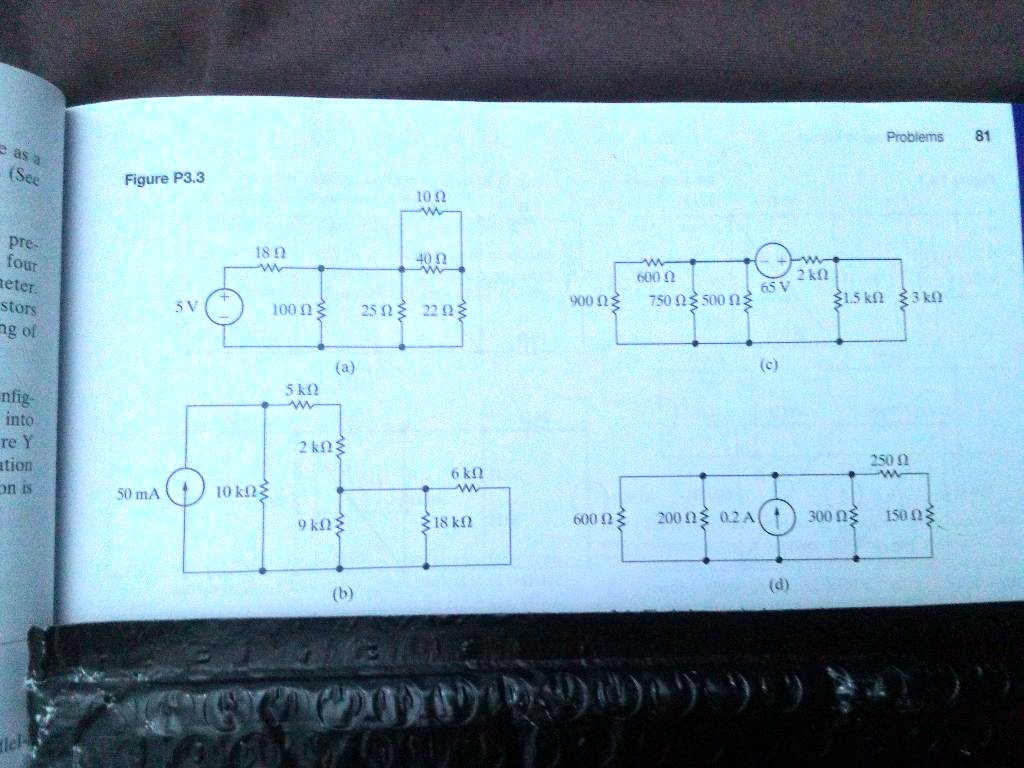
SOLVED For Each Of The Circuits Shown In Fig. P3.3, A) Identify
Practical Applications (Where the Rubber Meets the Road)
3. Real-World Scenarios
Okay, theory is great, but how does this apply in the real world? Let's consider a few practical scenarios. Imagine you need a 25-ohm resistor, but all you have are 100-ohm resistors. No problem! By connecting four 100-ohm resistors in parallel, you can achieve the desired 25-ohm resistance (100/4 = 25).
Another common application is in LED circuits. LEDs need a specific amount of current to operate correctly. Sometimes, the available resistors don't provide the exact current limiting needed. By using parallel resistors, you can fine-tune the resistance to get the LED's brightness just right without blowing anything up (always a good goal in electronics!).
Parallel resistors are also used in amplifier circuits to adjust gain or impedance matching. They can help to create a voltage divider with a lower overall resistance, allowing more current to flow through the circuit. This is useful when you need a specific voltage drop while maintaining a low impedance path.
Beyond the individual component level, parallel resistors are essential in power distribution networks. Large arrays of resistors are often used to dissipate heat evenly and provide a stable voltage supply to sensitive components. This is crucial in high-power applications where heat management is paramount.
Factors to Consider (It's Not Just About Resistance)
4. Wattage, Tolerance, and More
While calculating the equivalent resistance is crucial, it's not the whole story. You also need to consider the power rating (wattage) of the resistors. When resistors are connected in parallel, the current is divided among them. However, each resistor still dissipates power as heat, and you need to ensure that each resistor can handle its share of the power without overheating and potentially failing.
If the total power dissipated by the parallel combination exceeds the power rating of any individual resistor, you'll need to use higher wattage resistors or add more resistors to spread the load. It's generally good practice to choose resistors with a power rating that is at least twice the expected power dissipation to provide a safety margin.
Resistor tolerance is another important factor. Resistors aren't perfect; they have a certain percentage of error in their stated resistance value. If you need a very precise resistance, you'll need to use resistors with a low tolerance (e.g., 1% or 0.1%) and potentially measure the actual resistance of each resistor before connecting them in parallel.
Lastly, consider the physical size and layout of the resistors. In high-frequency circuits, the parasitic inductance and capacitance of the resistors can become significant. Shorter lead lengths and careful component placement can minimize these effects and improve circuit performance. The type of resistor (e.g., through-hole, surface mount) will also affect the physical layout and heat dissipation characteristics.
Combination Of Resistors In Series And Parallel Unifyphysics
Common Mistakes and How to Avoid Them
5. Troubleshooting Tips
One common mistake is forgetting to take the reciprocal after adding the reciprocals of the individual resistances. Remember, the formula gives you 1/Rtotal, not Rtotal directly! Always flip the fraction at the end to get the actual total resistance. A simple calculator app can come in handy here!
Another frequent error is neglecting the power rating of the resistors. Always calculate the power dissipation for each resistor in the parallel combination and ensure that it doesn't exceed the resistor's power rating. Using a resistor that's too small can lead to overheating, component failure, and potentially even a fire hazard. Safety first!
Also, be careful when mixing resistors with significantly different resistance values. If one resistor has a much lower resistance than the others, it will carry most of the current, effectively negating the effect of the other resistors. In such cases, you might need to use a different configuration or choose resistors with more similar values.
Finally, always double-check your calculations and circuit connections before applying power. A small mistake can have significant consequences, especially in high-power circuits. Use a multimeter to verify the resistance of the parallel combination and ensure that it matches your calculated value. Better safe than sorry!