Ace Tips About How To Create A XOR

Demystifying XOR

1. Unraveling the XOR Mystery

Ever stumbled across "XOR" and felt like you needed a secret decoder ring? Don't worry, you're not alone! XOR, short for "exclusive OR," sounds intimidating, but it's a fundamental logic gate that's surprisingly easy to understand. Think of it as a picky friend who only agrees when one of you suggests something, but not if you both do. In the world of computers, it's all about bits and bytes, but we'll break it down so even your grandma could grasp it (maybe!).

At its core, XOR is a comparison tool. It takes two inputs — let's call them A and B — and returns a 'true' (or 1) value if only one of the inputs is true. If both inputs are true, or if both are false, XOR returns 'false' (or 0). Imagine a light switch. XOR is like having two switches controlling one light. If only one switch is flipped, the light is on. If both are flipped, or neither is flipped, the light is off. Simple, right?

Why should you care? Well, XOR is a workhorse in the digital realm. It's used in cryptography for encryption, in error detection codes to ensure data integrity, and even in image processing for cool effects. So, understanding XOR opens doors to grasping how computers handle data securely and efficiently. And who knows, maybe you'll even impress your tech-savvy friends at your next get-together!

So, hold on tight, because we are about to dive into the world of binary and logic gates to master the art of creating XOR. Prepare to unlock a powerful tool in your coding arsenal!

Building Blocks

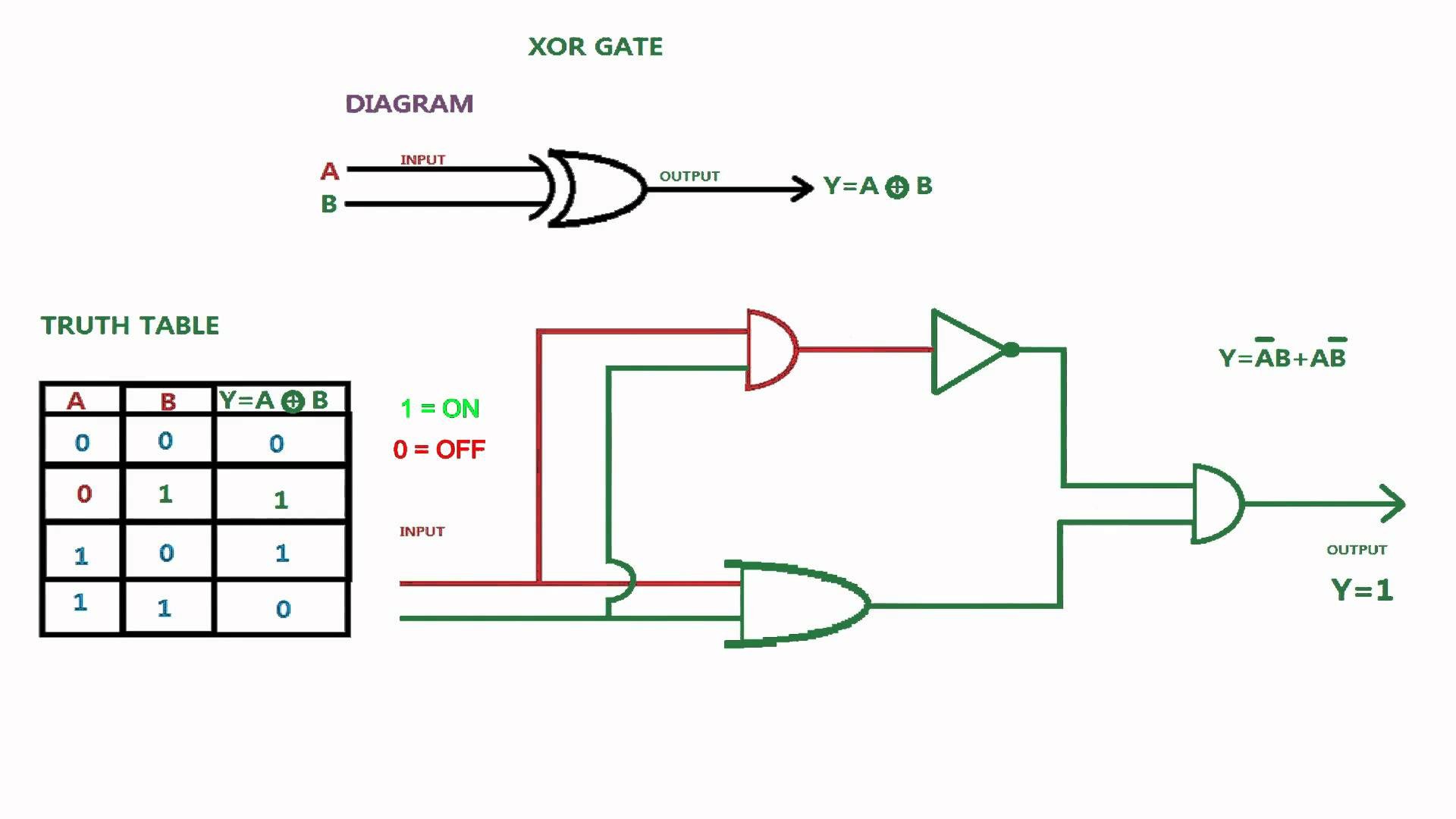
2. The XOR Truth Table

The best way to really "get" XOR is by visualizing it. Enter the truth table! This little table summarizes all the possible input combinations and their corresponding XOR output. Think of it as the Rosetta Stone for understanding XOR logic. Its the foundation upon which all XOR operations are built.

Here's what the XOR truth table looks like:

A | B | XOR------- | -------- | --------0 | 0 | 00 | 1 | 11 | 0 | 11 | 1 | 0

Pretty straightforward, huh? Notice that XOR outputs '1' only when A and B have different values. When they're the same (both 0 or both 1), XOR outputs '0'. This table is your constant companion, so keep it handy as we move forward.

Memorizing (or at least understanding) this truth table is crucial. It is the bedrock of understanding how XOR works. While seemingly simple, its impact is profound across computer science and digital electronics. Mastering this table means mastering the fundamental behavior of the XOR operation. So, embrace it, study it, and let it guide you through the XOR-filled adventures ahead.

Don't underestimate the power of simplicity! This table, in its compact form, contains the essence of XOR. From cryptography to error detection, the principles encapsulated in this truth table are applied time and time again. So, take a moment, appreciate its elegance, and commit it to memory. You'll thank yourself later!

Creating XOR with Other Gates

3. DIY XOR

Okay, so you've got the truth table down. Now, let's get our hands dirty and actually build an XOR gate. The cool thing is, you can create XOR using the more basic AND, OR, and NOT gates. Think of it like building a fancy Lego set with simpler bricks. This approach provides a deeper insight into how digital logic actually works.

The formula for creating XOR using AND, OR, and NOT is: (A AND (NOT B)) OR ((NOT A) AND B). Let's break that down: NOT A: Inverts the value of A (0 becomes 1, 1 becomes 0). NOT B: Inverts the value of B. (A AND (NOT B)): This part is true only if A is true and B is false. ((NOT A) AND B): This part is true only if A is false and B is true. OR: Finally, the OR gate combines the results of the two AND operations. If either of those AND operations is true, the XOR output is true.

This might seem complex written out, but picture it as a series of interconnected logic gates. The NOT gates flip the inputs, the AND gates check for specific conditions, and the OR gate combines the results. By stringing these gates together in this way, we achieve the same functionality as a dedicated XOR gate. It is a testament to the flexibility and power of boolean algebra!

Understanding how to synthesize XOR from these fundamental gates isn't just academic. It's incredibly practical. In some hardware implementations or low-level programming scenarios, you might not have a direct XOR operator available. Knowing how to construct it from AND, OR, and NOT allows you to implement XOR logic regardless. Furthermore, grasping this synthesis deepens your understanding of digital circuit design and optimization.

XOR in Programming: Code Examples

4. XOR in Action: Examples in Different Languages

Time to bring XOR to life with some code! Most programming languages have a built-in XOR operator, usually represented by the caret symbol (`^`). Let's see how it works in a few common languages.

Python:

a = Trueb = Falseresult = a ^ b  # result will be Trueprint(result)a = 5  # Binary: 0101b = 3  # Binary: 0011result = a ^ b  # result will be 6 (Binary: 0110)print(result)

In Python, `^` performs a bitwise XOR operation. Each bit of `a` is compared with the corresponding bit of `b`, and the result is calculated based on the XOR truth table. This makes it easy to manipulate individual bits within integers.

JavaScript:

let a = true;let b = false;let result = a ^ b; // result will be trueconsole.log(result);let x = 10; // Binary: 1010let y = 12; // Binary: 1100let z = x ^ y; // Binary: 0110, which is 6 in decimal.console.log(z)

JavaScript also uses the `^` operator for XOR, behaving similarly to Python. When used with boolean values, it returns a boolean. When used with numbers, it performs a bitwise XOR. It's a versatile operator for boolean and binary logic.

C++:

#include using namespace std;int main() {    bool a = true;    bool b = false;    bool result = a ^ b; // result will be true    cout << result << endl;    int x = 15; // Binary: 1111    int y = 5;  // Binary: 0101    int z = x ^ y;  // Binary: 1010, which is 10 in decimal.    cout << z << endl;    return 0;}

C++ treats `^` just like the other languages — a direct, bitwise XOR operation. Remember to include the `iostream` header for printing output in C++.

These examples demonstrate the simplicity and elegance of the XOR operator. Whether you're working with boolean logic or manipulating individual bits within integers, XOR provides a powerful and concise tool for accomplishing various tasks. Experiment with these examples, adapt them to your own code, and unlock the full potential of the XOR operator in your programming projects.

Practical Applications of XOR

5. XOR's Real-World Superpowers

Okay, we've covered the theory and the code. Now, let's talk about where XOR really shines in the real world. You might be surprised at how often this little logic gate pops up in important applications.

One of the most prominent uses of XOR is in cryptography . XOR is a crucial part of many encryption algorithms because of its reversibility. If you XOR a piece of data with a key, you can XOR the result with the same key again to get the original data back. This makes it ideal for simple encryption schemes. While modern encryption algorithms are far more complex, the basic principle of using XOR for encryption remains a fundamental concept.

Another key application is in error detection and correction . XOR is used to create parity bits, which are added to data to detect errors during transmission. By calculating the XOR of all the bits in a data packet, a parity bit can be generated. If, upon receiving the data, the XOR of the data bits and the parity bit doesn't match, an error has occurred. While more sophisticated error correction codes exist, XOR-based parity checking is a simple and effective way to detect common transmission errors.

XOR also finds its way into graphics and image processing . For example, XOR can be used to draw or erase objects on a screen without needing to redraw the entire background. By XORing the object with the background, you draw it. XORing it again with the same location erases it, restoring the original background. This technique can be used to implement simple animation effects efficiently.

From cryptography to error correction to graphics, XOR is a versatile tool with a wide range of practical applications. Its simplicity and reversibility make it an ideal component in many digital systems. By understanding the power of XOR, you unlock a fundamental building block in computer science and digital electronics.